Die exakte Bestimmung der effektiven Dosis im Körper einer Person die sich in einem Strahlenfeld aufhält, ist nur mit Hilfe von komplizierten Dosisberechnungen möglich. Selbst im Fall einer homogenen Bestrahlung des menschlichen Körpers, bei der sich der ganze Körper in einem homogenen Strahlenfeld befindet, ist die resultierende Dosisverteilung im Körper alles andere als homogen. Aus diesem Grund wird im Strahlenschutz zur Bestimmung der Dosis auf messbare und gut zugängliche Grössen zurückgegriffen. Eine dieser Grössen ist die Ortsdosis. Sie lässt sich zum Beispiel mithilfe von Ortsdosisleistungsmessgeräten direkt messen und gibt einen Schätzwert der effektiven Dosis für eine Person, die sich an einem bestimmten Ort im aufgeweiteten Strahlenfeld aufhält. Atome zerfallen unterschiedlich, die von ihnen ausgehende Strahlung hat nicht die gleiche Wirkung auf den Menschen. Deshalb werden Umrechnungsfaktoren benötigt, die diesen Umstand berücksichtigen.
[caption id="attachment_24152" align="alignnone" width="700"]
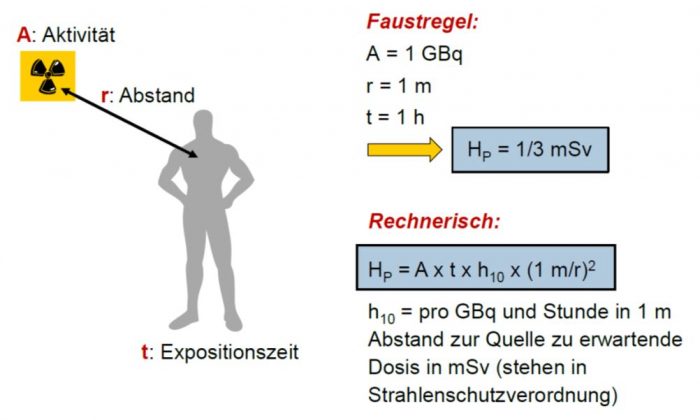
Figur 139-1: Grundsätzliche Zusammenhänge bei der Bestimmung der auf einen Menschen wirkenden Dosis. Die Aktivität, der Abstand des Menschen zur radioaktiven Quelle und der Umrechnungsfaktor h10, der die von Atomsorte abhängige Strahlenenergie berücksichtigt.[/caption]
Mit den in der Strahlenschutzverordnung aufgelisteten, nuklidspezifischen Umrechnungsfaktoren h10 können Aktivitäten direkt in Ortsdosisleistungen umgerechnet werden. Der Faktor h10 wird verwendet, um die Dosisleistung in 10 mm Gewebetiefe in 1 m Abstand von einer radioaktiven Quelle mit einer Aktivität von 1 Giga-Bequerel (109 Bq) zu berechnen. Diese Umrechnungsfaktoren (h10) sind für die vielen Atomsorten in der Strahlenschutzverordnung, Anhang 3 über 32 Seiten (Seiten 81 bis 113) aufgelistet.
Für radioaktive Quellen gilt allgemein, dass die Dosisleistung proportional zur Aktivität ist und mit zunehmendem Abstand zur Quelle rasch (quadratisch) kleiner wird (Figur 139-2).
[caption id="attachment_24153" align="alignnone" width="700"]
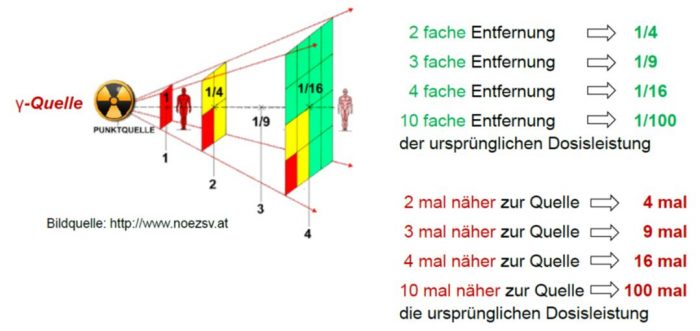
Figur 139-2: Die Dosis nimmt quadratisch zu, wenn man sich der Quelle nähert. Sie nimmt quadratisch ab, wenn man sich entfernt. Befindet man sich in 4facher Entfernung, ist die Dosis 16mal kleiner.[/caption]
Um für dieses hypothetische, unrealistische Gedankenexperiment Ortsdosisleistungen zu berechnen, wurden in den unten beschriebenen Berechnungen die Umrechnungsfaktoren h10 aus der Strahlenschutzverordnung und die von der Nagra angegebenen Nuklid-Inventare verwendet (siehe Antwort zu Frage 138). Berechnet werden die Dosen pro Stunde gemäss Inventar (GBq) × h10 (mSv/Stunde/GBq). Die Dauer, in welcher die letale Dosis von 6000 mSv erreicht wird, kann mittels der Formel 6000 mSv / (Inventar × h10) berechnet werden.
Die Nagra gibt in NTB 02-05, Seite B-5, ein 137Cs-Inventar von 3,4×1015 Bq in den Endlagerbehältern für abgebrannte DWR-Brennelemente an. Es zeigt sich, dass das Nuklid 137Cs die berechneten Dosen dominiert (siehe Tabelle 139-1), die Beiträge der anderen Nuklide sind im Vergleich zu 137Cs deutlich geringer. Die von der Nagra vorgesehenen Behälter für verglaste hochaktive Abfälle enthalten ähnliche Inventare an 137Cs. Mit den in der Antwort zu Frage 138 angegeben Inventaren können die jeweiligen hypothetischen Dosen berechnet werden. Im angesprochenen hypothetischen, unrealistischen Fall würde für das Inventar eines Endlagerbehälters für 4 DWR-Brennelemente eine letale Dosis von 6000 mSv im Abstand von einem Meter innert weniger als 2 Minuten erreicht.
Die Brennelemente sind gemäss der Richtlinie ENSI-G03 in den Endlagerbehältern bis zu 1000 Jahre komplett einzuschliessen. Wiederholt man das obige Gedankenexperiment nach 1000 Jahren ist das 137Cs aufgrund seiner Halbwertszeit von rund 30 Jahren zum grössten Teil zerfallen und die Dosis im Vergleich zu anderen Nukliden unbedeutend geworden.
[caption id="attachment_23098" align="alignnone" width="700"]
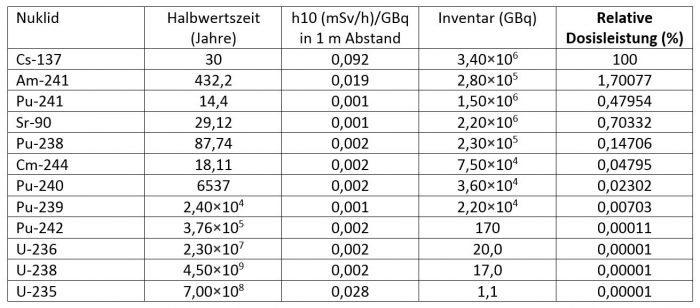
Tabelle 139-1: Das
137Cs-Inventar in Endlagerbehältern für abgebrannte DWR-Brennelemente beträgt 3,4×10
9 GBq. Das Nuklid
137Cs ist dosisdominierend. Das nächste Nuklid,
241Am erreicht nur rund 2 % der Wirkung von
137Cs.[/caption]
Im in der Frage 139 betrachteten Fall ist also der Beitrag von 137Cs dominant (Figur 139-3). Die Halbwertszeit von 137Cs beträgt ungefähr 30 Jahre. Die Dosis beträgt deshalb nach 30 Jahren die Hälfte und nach 60 Jahren ein Viertel. Die Brennelemente sind gemäss der Richtlinie ENSI-G03 in den Endlagerbehältern bis zu 1000 Jahre komplett einzuschliessen. Nach 1000 Jahren ist das 137Cs aufgrund seiner Halbwertszeit von rund 30 Jahren zum grössten Teil zerfallen und die Dosis im Vergleich zu den Nukliden wie 241Am unbedeutend geworden.
[caption id="attachment_24154" align="alignnone" width="700"]
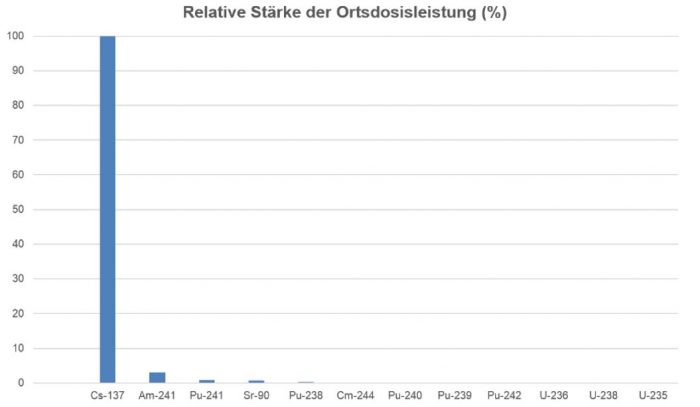
Figur 139-3: Im in Frage 139 betrachteten Fall ist der Beitrag von
137Cs dominant. Der Anteil des nächststärksten Nuklids (Atomsorte)
241Am beträgt bloss einige Prozent.[/caption]
In Figur 139-4 wird die zeitliche Entwicklung des Beitrags von 137Cs zur Ortsdosisleistung gezeigt. Aufgrund der verwendeten linearen Darstellung (jeweils gleiche Abstände in der Zeit und in der Dosis) kann der Eindruck erweckt werden, dass die Aktivität nach rund 300 Jahren verschwunden ist. Dies ist nicht der Fall.
[caption id="attachment_24155" align="alignnone" width="700"]
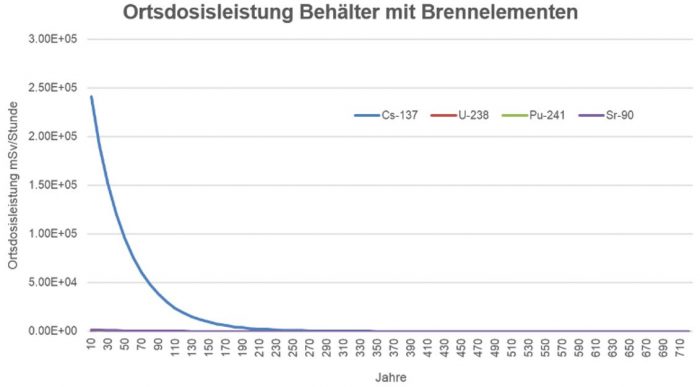
Figur 139-4: Zeitliche Entwicklung des Beitrags von
137Cs zur in Frage 139 diskutierten Ortsdosisleistung.[/caption]
Deshalb wird in Darstellungen der zeitlichen Entwicklung der Radioaktivität von Abfällen die logarithmische Darstellung verwendet. In Figur 139-5 wird nun die Ortsdosisleistung nicht mehr in gleichen Abständen aufgetragen, sondern jeweils in Faktoren von 100. Wo in Figur 139-4 für die Ortsdosisleistungen 0, 50‘000, 100‘000, 150‘000, 200‘000 und 250‘000 als Achsenbeschriftungen verwendet wurden, wird in Figur 139-5 der Schritt immer um jeweils den Faktor 100 verkleinert. Von 1‘000‘000 zu 10‘000, dann zu 100, dann zu 1, dann zu 0.01, etc. Dies erlaubt es, die jeweiligen Beiträge zur Dosis über die gesamte Zeit genau abzubilden. Die Darstellung ist damit aussagekräftiger und wird deshalb in Publikationen des ENSI und der Nagra verwendet.
[caption id="attachment_24156" align="alignnone" width="700"]

Figur 139-5: Wie in Figur 139-4 werden die zeitlichen Entwicklungen der Beiträge von
137Cs und weiteren radioaktiven Stoffen zur in Frage 139 diskutierten Ortsdosisleistung aufgetragen. Im Unterschied zu Figur 139-4 sind nun alle Beiträge von allen Stoffen über die ganze Zeitperiode gut ablesbar.[/caption]
Aufgrund der unterschiedlichen Halbwertszeiten der Nuklide ändert sich ihr jeweiliger Beitrag zur Radiotoxizität (Figur 139-6). Die Nagra hat in NTB 02-05, Seite 192, den zeitlichen Verlauf der Radiotoxizität für abgebrannte Brennelemente (oben) und verglaste hochaktive Abfälle (unten) aufgetragen.
[caption id="attachment_24043" align="alignnone" width="700"]

Figur 139-6: Anteil der verschiedenen Radionuklide zur Radiotoxizität für das Inventar der abgebrannten Brennelemente (oben) und der verglasten hochaktiven Abfälle (unten). Die Aktivität [Bq] kann aus dem Radiotoxizitätsindex (RTI) wie folgt berechnet werden: Aktivität gleich 10
-4 Sv mal RTI geteilt durch den Dosiskoeffizienten [Sv/Bq] für Ingestion für das betreffende Nuklid. Die Dosiskoeffizienten sind in der Strahlenschutzverordnung tabellarisch für die jeweiligen Nuklide aufgeführt. Im Falle von
137Cs zum Zeitpunkt von 1 Jahr findet man für alle abgebrannten Brennelemente RTI=10
15, e
ing=1,3×10
-8 Sv/Bq und somit ein Inventar an
137Cs von rund 7,8×10
18 Bq. Quelle: NTB 02-05, Seite 192.[/caption]
Referenzen
NTB 02-05: Project Opalinus Clay: Safety Report – Demonstration of Disposal feasibility for spent fuel; vitrified high-level waste and long-lived intermediate level waste (Entsorgungsnachweis), Nagra Technischer Bericht, Wettingen, 2002.
ENSI-G03 Spezifische Auslegungsgrundsätze für geologische Tiefenlager und Anforderungen an den Sicherheitsnachweis. Eidgenössisches Nuklearsicherheitsinspektorat, Brugg






